My final important step in the development of incommensurate theory involved an appreciation of the fact that it must be compatible with translational symmetry, specifically in relation to atom displacement in the order-disorder processes existing in the plagioclase feldspars and elsewhere. In a paper on the incommensurate behavior in the plagioclase feldspars, in the Can. Min. (2008) , 46 1389-1400, I used the pair of conventional Abelian exponential translation matrices exp ± ik.r, in a similarity transformation, to obtain the pair of real orthogonal Lie SO(2 ) group matrices which together form the continuous Lie group O(2). Here r and k= 2π/λ are vectors, and k,r is simply an inner product which yields a phase angle in the range 0 to 2π.
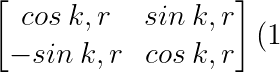\:&space;\:&space;and&space;\begin{bmatrix}cos\:&space;k,r&space;&&space;-sin&space;\:&space;k,r\\&space;sin\:&space;k,r&space;&&space;cos\:&space;k,r&space;\end{bmatrix}&space;(2))
These Abelian matrices have determinant +1. They form the basis of the representation tables for two new translation groups described in my paper of 2008. Matrices (1) and (2) are inverse and hence describe translations in direction ± r respectively They combine to form the non-Abelian Lie group O(2). Note, for future reference, that all the possible matrices in the SO(2) Lie groups commute. Also, that Eugene P. Wigner, in Group Theory, 1959 Academic Press, Chapter 14 developed the rotational dihedral groups in exactly the same manner. In the present case the paired Abelian components of each of these matrices describe the probability amplitudes of two independent functions associated with cosine and sine terms, and thus provide a pair of k wave functions defining displacements in terms of the general field of quantum mechanics. However, in this version of quantum mechanics we use the cosine function initially to define position on displacement, and the sine function to describe the associated gradient of position.
At this point we note that our new mathematical definition of quantum behaviour, as related to translational symmetry, makes no reference to either mass or velocity and may be adapted for use in a wide range of stationary problems including order-disorder and incommensurate behaviour.
In the latter case we must now understand immediately the significance of the independent e and f systems of reflections, already described, in the plagioclase feldspars. They represent the two interacting order-disorder functions, cos (k,r) and sin (k,r) which our formative mathematical theory links to the Abelian SO(2) Lie groups.